lunes, 12 de enero de 2015

Actividades del sistema de coordenadas

Entra al siguiente linck :

http://www.gobiernodecanarias.org/educacion/4/Medusa/GCMWEB/Code/Recursos/VisualizarPagina.aspx?IdRecurso=5488

y resuelve las actividades, recuerda capturar pantalla y enviármela por facebook

Sistema de coordenadas cartesianas

Un sistema de coordenadas cartesianas lo forman dos ejes perpendiculares entre sí, que se cortan en el origen.

Las coordenadas de un punto cualquiera vendrán dadas
por las proyecciones de la distancia entre el punto y el origen
sobre cada uno de los ejes.

Ejes de coordenadas

Al sistema de coordenadas también se le llama ejes de
coordenadas o ejes cartesianos.

El eje horizontal se llama eje X o eje de abscisas.

El eje vertical se llama eje Y o eje de ordenadas.

El punto O, donde se cortan los dos ejes, es el origen de coordenadas.

Las coordenadas de un punto cualquiera P se representan por (x, y).

La primera coordenada se mide sobre el eje de abscisas, y se la
denomina coordenada x del punto o abscisa del punto.

La segunda coordenada se mide sobre el eje de ordenadas, y se le
llama coordenada y del punto u ordenada del punto.

Los ejes de coordenadas dividen al plano en cuatro partes
iguales y a cada una de ellas se les llama cuadrante.

Signos

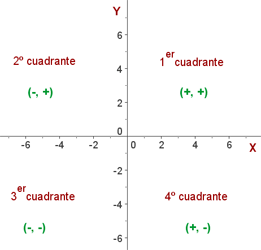
	Abscisa	Ordenada
1^ercuadrante	+	+
2º cuadrante	−	+
3^ercuadrante	−	−
4º cuadrante	+	−

El origen de
coordenadas, O, tiene
de coordenadas: O(0, 0).

Los puntos que están
en el eje de ordenadas
tienen su abscisa igual a 0.

Los puntos situados en el
eje de abscisas tienen su
ordenada igual a 0.

Los puntos situados en
la misma línea horizontal
(paralela al eje de abscisas)
tienen la misma ordenada.

Los puntos situados en
una misma línea vertical
(paralela al eje de ordenadas)
tienen la misma abscisa.

A(1, 4), B(-3, 2), C(0, 5), D(-4, -4), E(-5, 0), F(4, -3), G(4, 0), H(0, -2)

jueves, 4 de diciembre de 2014

Examen piloto

Matemáticas
Ejercicio de simulación

1.- ¿cuál es la serie que da respuesta correcta a la siguiente cuestión?

X.- novecientos veinticinco mil ciento veintiséis ( ) 92 500 126
y.- noventa y dos millones quinientos

Doce mil seiscientos ( ) 925 126
z.- noventa y dos millones quinientos mil ciento veintiséis ( ) 92 512 600

a) z, y, x b) y, z, x c) x, y, z

2.- ¿opción que nos ordena los números de mayor a menor?

A) 89 216 126 b) 594 316 121 c) 937 000 001
594 316 121 89 216 126 89 216 126
937 000 001 937 000 001 594 316 121
3.- ¿opción que nos ordena los números de menor a mayor?

A) 100 378456 b) 123 000 379 c) 100 378 456
123 456 778 123 456 778 123 000 379
123 000 379 100 378 456 123 456 778

4.- ¿cuál es la media y mediana de la siguiente serie?
36, 38, 40, 41, 44, 46, 49

a) media: 43 b) media: 40 c) media: 42
mediana: 44 mediana: 41 mediana: 41
5.- ¿cuál es la serie que descompone correctamente 15 210 mm?

A) 15.21 m b) 1.521 m c) 152.1 m
152.1 dm 152.1dm 15.21dm
1521 cm 15.21cm 1.521cm

6.- ¿compara las longitudes es la correcta?

A) 4 955 dam < 494 hm b) 5 261 m > 36 km c) 39 476 < 39 476 146 dm

7.- ¿cuál es la pirámide que tiene cuatro caras triangulares iguales?

A) trapezoidal b) rectangular c) cuadrangular

8.-resuelve los problemas
juan cosecho 421.583 kg de trigo, 823.043 kg de cebada y 127.98 kg. De frijol. ¿Cuantos kg cosecho en total?

A) 1372.606 kg b) 137.726 06 kg c) 13 726.06 kg

9.-Antonio necesita $ 959.50 pesos, hasta hoy lleva ahorrados $ 568.25 ¿cuanto le falta por ahorrar?

A) $ 389.35 b) $ 391.25 c) 395.21

10.- ¿cuál de las siguientes divisiones está resuelta correctamente?

A) 1230 entre 4= 308 b) 3980 entre 25 = 159 c) 450 entre 5 = 95

11.- realiza una tabla de conversión de unidades.

12.- ¿compara las siguientes medidas y selecciona la correcta?

A) 216.3 kg > 0.2761kg b) 2389kg < 0.23891kg c) 2389kg > 0.2389kg

13.-un grupo de 24 personas obtuvo un premio de $ 1 830.00 si se reparten equitativamente ¿cuanto le corresponde a cada persona?

A) $67.52 b) $72.65 c) $ 76.25

14.-en un salón de 32 estudiantes, el 12.5 % está enfermo ¿cuantos estudiantes están enfermos?

A) 4 estudiantes b) 9 estudiantes c) 6 estudiantes

15.-pedro tenia $ 980.00 y gasto $ 245.00 ¿que porcentaje del dinero que tenia, se gasto Pedro?

A) 30% b) 25% c) 28%

16.-una escuela compro 13 computadoras iguales y pago $ 76 351.50 ¿cuál fue el precio de cada computadora?

A) $ 7 812.00 b) $ 5 873.15 c) $ 6 321.45

17.- ¿5 es divisor de…?

A) 20, 72, y 90

B) $ 12, 30, y 84 c) 100, 25 y 80

18.-don Joaquín cosecho 19,890 aguacates y quiere empacarlos en cajas con 30 espacios, ¿cuántas cajas llenará en total?

A) 660 cajas b) 663 cajas c) 666 cajas

19.-diana compro 4 faldas de los siguientes colores: azul, blanco, café y negro; además 6 blusas diferentes. ¿Cuántas combinaciones posibles podrá realizar?

A) 10 combinaciones b) $ 24 combinaciones c) 4 y sobran 2 blusas

20.- ¿cuales coordenadas forman un triangulo?

A) (2,3) (4,5) (6,7)
b) (2,2) (4,6) (6,2)
c) (2,3) (4,3) (6,3)

lunes, 17 de noviembre de 2014

área y perímetro

PERÍMETRO Y ÁREA DEL CUADRADO

	PERÍMETRO El perímetro de un cuadrado es cuatro veces el valor del lado P = 4 · a
	ÁREA El área de un cuadrado es igual al cuadrado de la longitud del lado. A= a²

PERÍMETRO Y ÁREA DEL RECTÁNGULO

	PERÍMETRO El rectángulo tiene los lados iguales dos a dos, por tanto: P = 2· a + 2· b
	ÁREA El área de un rectángulo es el producto de la longitud de los lados. A= a · b

Ejercicios

1.- Calcula el perímetro y el área de un cuadrado de lado 4 m.

2.- La base de un rectángulo es 5 m. y la altura la mitad de la base. Calcula el área y el perímetro.

3.- El área de un cuadrado es 5,76 cm² . Calcula el perímetro del cuadrado

Cómo hacer un croquis

Materiales:

Cartulina, hoja de papel, lápiz, borrador.

Indicaciones:

1.- Dibuja una línea recta que representará tu casa, este es el punto de partida.

2.- Dibuja un rectángulo por cada cuadra que avances en línea recta durante tu trayecto hacia la escuela.

3.- Indica el sitio en el que cambias la dirección de tu trayecto.

4.- Señala los lugares importantes por dónde transitas para que sirvan como referencia en tu trayecto.

5.- Escribe los nombres de las calles por donde pasas en tu trayecto a la escuela.

Como último paso debes escribir las indicaciones para realizar el trayecto, por ejemplo:

1.- Camina tres cuadras hacia la derecha de la casa, verás una tienda.

2.- Da vuelta a la izquierda y avanza por cuatro cuadras, te encontrarás con una glorieta.

3.- Atraviesa la calle, encontrarás un parque.

5.- Sigue derecho, después del parque encontrarás la escuela.

fracciones impropias y mixtas

Fracciones impropias

	Definición rápida: una fracción impropia tiene su numerador (número de arriba) mayor o igual que su denominador (número de abajo), 7/4 o 4/3 ("pesa más arriba")
7/4
(siete cuartos)

Fracciones

Una fracción (como 7/4) tiene dos números:

Numerador

Denominador

Al número de arriba lo llamamos Numerador, es el número de partes que tenemos.
Al número de abajo lo llamamos Denominador, es el número de partes en que hemos dividido el total.

Hay tres tipos de fracciones:

Fracciones propias:	El numerador es menor que el denominador
Fracciones propias:	Ejemplos: 1/3, 3/4, 2/7

Fracciones impropias:	El numerador es mayor (o igual) que el denominador
Fracciones impropias:	Ejemplos: 4/3, 11/4, 7/7

Fracciones mixtas:	Un número entero y una fracción propia juntos
Fracciones mixtas:	Ejemplos: 1 1/3, 2 1/4, 16 2/5

Fracciones impropias

Entonces, una fracción propia es sólo una fracción donde el numerador (el número de arriba) es más grande o igual que el denominador (el número de abajo). O sea, arriba pesa más.

Ejemplos

3/2

7/4

16/15

Fracciones impropias = Fracciones mixtas

Puedes usar una fracción impropia o una fracción mixta para escribir la misma cantidad. Por ejemplo 1 3/4 =7/4, aquí se ve:

1 3/4		7/4
	=

¿Las fracciones impropias son malas?

¡NO, no son malas! De hecho en matemáticas son mejores que las fracciones mixtas. Las fracciones mixtas se confunden cuando las escribes en una fórmula:

Fracción mixta:	¿Cuánto es:	1 + 2 1/4	?
	¿Es:	1+2+1/4	= 3 1/4 ?
	¿O es:	1 + 2 × 1/4	= 1 1/2 ?

Fracción impropia:	¿Cuánto es:	1 + 9/4	?
	Es:	4/4 + 9/4 = 13/4

Pero, para el uso de cada día, la gente entiende mejor las fracciones mixtas. Es más fácil decir "me comí 2 1/4salchichas" que "me comí 9/4 salchichas"

Pueden ser iguales

¿Qué pasa cuando el numerador y el denominador son iguales? Por ejemplo 4/4?

Bueno, está claro que es un entero, pero está escrito en forma de fracción, así que la gente dice que es una fracción impropia.

Convertir fracciones impropias en fracciones mixtas

Para convertir una fracción impropia en mixta, sigue estos pasos:

Divide el numerador entre el denominador.
Escribe el cociente como un número entero.
Después escribe el resto encima del denominador.

Ejemplo: Convierte 11/4 en una fracción mixta.

Divide: 11 ÷ 4 = 2 con resto 3
Escribe el 2 y después escribe el resto (3) encima del denominador (4), así:

2	3

	4

Convertir fracciones mixtas en fracciones impropias

Para convertir una fracción mixta en impropia, sigue estos pasos:

Multiplica la parte entera por el denominador.
Súmalo al numerador.
Después escribe el resultado encima del denominador.

Ejemplo: Convierte 3 2/5 en fracción impropia.

Multiplica la parte entera por el denominador: 3 × 5 = 15
Súmalo al numerador: 15 + 2 = 17
Después escribe el resultado encima del denominador, así:

Fracciones propias

	Definición rápida: Una fracción propia tiene su numerador (número de arriba) menor que su denominador (número de abajo), como 3/8 o 4/5
3/8
(Tres octavos)