Para escribir el número en cifras estas deben separarse con espacios en blanco cada 3 cifras. Es decir el siguiente número 45689791949 debe escribirse así: 45 689 791 949. En su defecto lo mas conveniente es separarlo por comas ejemplo:45,689,791,949.
Escritura y lectura en palabras de números grandes.
Para poder leer y escribir con palabras números grandes compuestos de muchas cifras usamos las escalas numéricas. Las escalas numéricas nos permiten clasificar las cifras de los números de 3 en 3 cifras, tomando en cuenta el orden de las cifras. Esta clasificación se hace con el propósito de facilitar la lectura y escritura del número en palabras. Existen dos tipos de escalas la larga y la corta.
Escala numérica larga.
Las cifras de un número en esta escala, se clasifican de 3 en 3, y a cada grupo se denomina clase. Dentro de cada clase la cifra de primer orden se conoce como unidad, la de segundo orden como decena y la de tercer orden como centena.
Un periodo esta formado por dos clases, es decir 6 cifras forman un periodo. Dentro de cada periodo, la clase de la izquierda es decir la clase de segundo orden se denomina millar o mil.
Los periodos a partir del segundo se denominan como millón, billón, trillón, cuatrillón, quintillón, sextillón, septillón, octillón, etc. pero en la práctica sólo se suele usar hasta el cuatrillón.
por ejemplo.
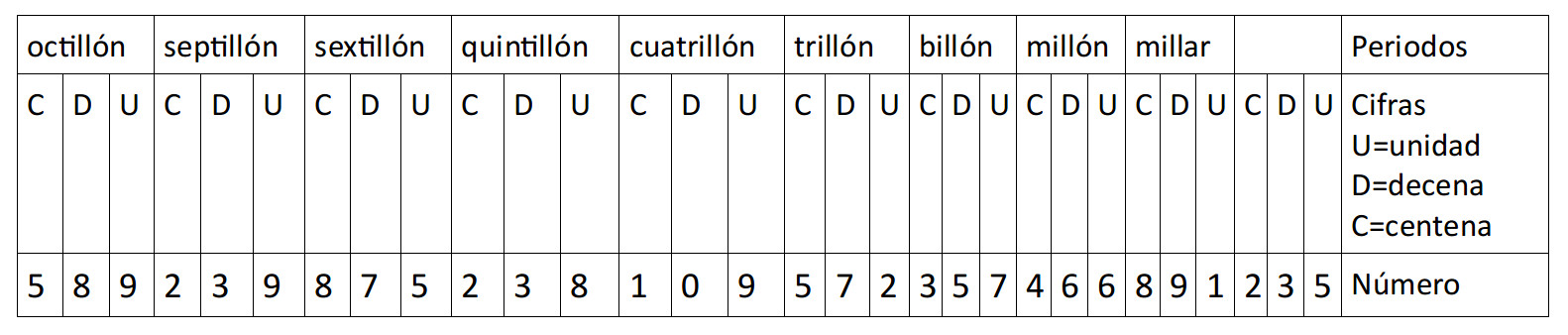
El número: 589 239 875 238 109 572 357 466 891 235 se clasifica del siguiente modo, antes de leerlo o escribirlo con palabras.
Escala numérica corta.
En la escala corta las cifras de los números se agrupan de 3 en 3, pero no se consideran las clases, y un grupo de 3 cifras determinan un periodo. Es decir una clase de la escala numérica larga es un periodo de la escala numérica corta. Dentro de cada periodo la cifra de primer orden se conoce como Unidad, la de segundo orden como decena y la de tercer orden como centena. Y los periodos se denominan a partir del segundo cómo: millar, millón, billón, trillón, cuatrillón, quintillón, sextillón, septillón, octillón, etc.
Por ejemplo.
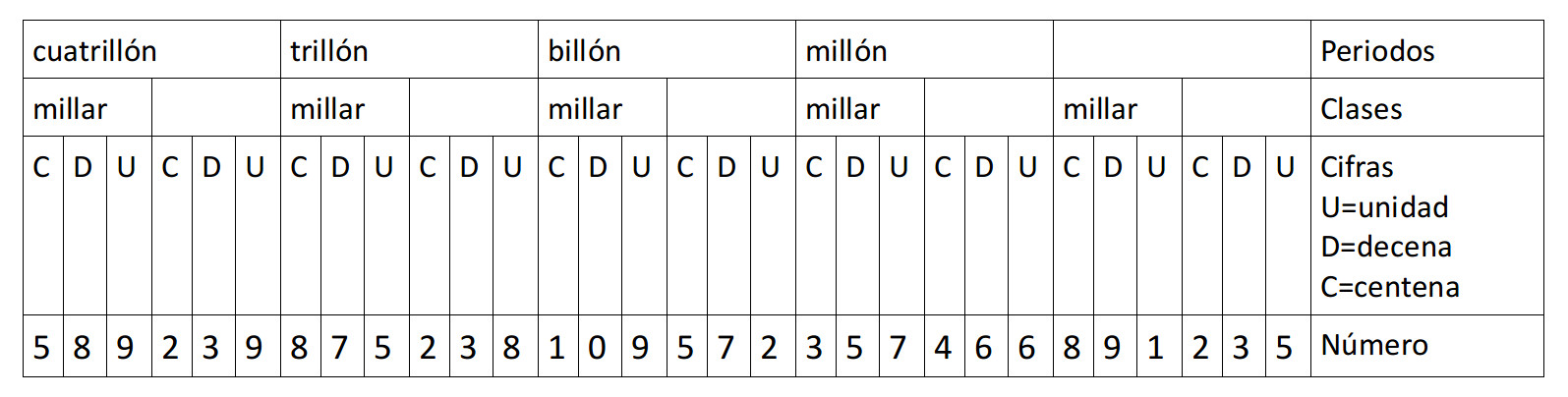
El número: 589 239 875 238 109 572 357 466 891 235 se agrupa o clasifica del siguiente modo, antes de leerlo o escribirlo con palabras.
Palabras que se usan para escribir números.
Para la escritura con palabras de los números menores al millón, en español tenemos las siguientes palabras que se usan paraescribir los números. Estas palabras hasta el millón se usan para ambas escalas.
| Números | Se escribe. | Descripción |
| 0 | cero | |
| 1 | uno | Femenino: una. |
| 2 | dos | |
| 3 | tres | |
| 4 | cuatro | |
| 5 | cinco | |
| 6 | seis | |
| 7 | siete | |
| 8 | ocho | |
| 9 | nueve | |
| 10 | diez | |
| 11 | once | |
| 12 | doce | |
| 13 | trece | |
| 14 | catorce | |
| 15 | quince | |
| 16 | dieciséis | |
| 17 | diecisiete | |
| 18 | dieciocho | |
| 19 | diecinueve | |
| 20 | veinte | |
| 21 | veintiuno |
Delante de un sustantivo:
masculino: veintiún
femenino: veintiuna.
|
| 22 | veintidós | |
| 23 | veintitrés | |
| 24 | veinticuatro | |
| 25 | veinticinco | |
| 26 | veintiséis | |
| 27 | veintisiete | |
| 28 | veintiocho | |
| 29 | veintinueve | |
| 30 | treinta |
Para números que tienen la cifra de primer orden distinto de 0. La escriturase conjuga con la letra y.
Ejemplos.
58 cincuenta y ocho. (50+8)
75 setenta y cinco. (70+5)
41 cuarenta y uno. (40+1)
99 noventa y nueve. (90+9)
Si la cifra de primer orden es 1 y el número se escribe delante de un sustantivo, entonces se conjuga con “y un” para masculino “y una”femenino.
Ejemplos.
Son cuarenta y un cigarrillos.
Son cincuenta y una señoritas. |
| 40 | cuarenta |
| 50 | cincuenta |
| 60 | sesenta |
| 70 | setenta |
| 80 | ochenta |
| 90 | noventa |
| 100 | cien (to) | |
| 101 | ciento uno | Femenino: ciento una. |
| 102 | ciento dos | |
| 200 | doscientos |
Para números como 545, 201, 458, 115, 999 etc. se escriben del siguiente modo:
545 quinientos cuarenta y cinco (500+40+5)
201 doscientos uno (200+1)
458 cuatrocientos cincuenta y ocho (400+50+8)
115 ciento quince. (100+10+5)
999 novecientos noventa y nueve. (900+90+9)
Femenino: Se cambia la terminación “os” por “as”.
Ejemplo.
cuatrocientas, quinientas, seiscientas, etc.
|
| 300 | trescientos |
| 400 | cuatrocientos |
| 500 | quinientos |
| 600 | seiscientos |
| 700 | setecientos |
| 800 | ochocientos |
| 900 | novecientos |
| 1000 | mil (millar) |
Se usa la palabra mil y es invariable hasta llegar al millón.
Ejemplos.
1002 mil dos.
2050 dos mil cincuenta.
12 548 doce mil quinientos cuarenta y ocho.
101 358 ciento un mil trescientos cincuenta y ocho.
999 999 novecientos noventa y nueve mil novecientos noventa y nueve
|
| 10 000 | diez mil |
| 100 000 | cien mil |
Si queremos escribir el número en palabras o leerlo, no es necesario crear una tabla para poder identificar los periodos y las clases, estas se pueden separar usando subindices o superindices.
Ejemplo.
para escribir en palabras el número: 589 239 875 238 109 572 357 466 891 235, en la escala numérica larga, se vuelve aescribir el número en cifras pero separando con un subindice o superindice los periodos.
5892394875238310957223574661891235. (con superindice)
5892394875238310957223574661891235. (con subindice)
Luego se procede a la lectura o escritura del número en palabras. "Quinientos ochenta y nueve mil doscientos treinta y nueve cuatrillones ochocientos setenta y cinco mil doscientos treinta y ocho trillones ciento nueve mil quinientos setenta y dos billones trescientos cincuenta y siete mil cuatrocientos sesenta y seis millones ochocientos noventa y un mil doscientos treinta y cinco".
Del mismo modo para la escala numérica corta se procede a colocar los subindices o superindices, pero en este caso los periodos son cada 3 cifras, y se empiezan a numerar a partir del segundo periodo, dejando sólo un espacio en blanco para separar el primer periodo.
58982397875623851094572335724661891 235. (con superindice)
58982397875623851094572335724661891 235. (con subindice)
Luego se procede a la lectura o escritura del número en palabras. "Quinientos ochenta y nueve octillones doscientos treinta y nueve septillones ochocientos setenta y cinco sextillones doscientos treinta y ocho quintillones ciento nueve cuatrillones quinientos setenta y dos trillones trescientos cincuenta y siete billones cuatrocientos sesenta y seis millones ochocientos noventa y un mil doscientos treinta y cinco".